(濰坊愛普環保設備有限公司)
摘 要 本文主要通過自由淹沒射流理論研究除塵器設計的相關課題。
關鍵詞 自由射流 噴管 擴張角
1 自由淹沒射流的基本流動特性
一股速度很大的流動射入周圍流體時所形成的流動,稱之為射流。射流周圍的流體本身具有速度時稱為伴隨射流,當周圍流體處于靜止狀態時,則稱為自由射流。射流將一部分動量傳遞給帶入的流體,因而射流的速度逐漸降低。最后射流的動量全部消失在空間流體中,射流也在靜止流體中淹沒了,所以又稱它為自由淹沒射流。
射流一般分為初始段和基本段兩部分。圖1所示為自由射流的結構示意圖。
假定流體以超過臨界速度的初速度U0均勻地從噴管出口流出,在流動中由于周圍流體的不斷摻入,射流的寬度逐漸增大,而在射流中還保持射流初速U0的區域(稱為射流核心區)則逐漸縮小。在離開噴管出口一定距離以后,保持初速U0的射流核心區就消失了。射流核心區完全消失的橫截面稱為轉折截面。在噴管出口與轉折截面之間的射流段稱為初始段,射流核心區就在初始段中。在轉折截面以后的射流段稱為基本段,在基本段中軸向流速逐漸減小,最后到零。射流與靜止流體的交界面(流速為零)稱為外邊界面,軸向流速還保持初速U0的邊界面(射流核心區的邊界面)稱為內邊界面。在內、外邊界面之間的區域稱為射流邊界層,在轉折截面以后整個射流都變成射流邊界層。射流外邊界現的交點O稱為射流極點,它的位置在噴管內。外邊界線之間的夾角θ稱為射流極角,也稱為射流擴散角。
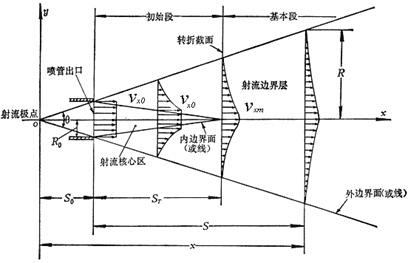
圖1 自由射流的結構示意圖
剪切射流符合邊界層的特點:射流邊界層的寬度小于射流的長度,即橫向尺度遠小于縱向尺度;在射流邊界層的任何橫截面上,橫向速度遠小于縱向速度;沿射流邊界層橫截面上的壓強是近似不變的,又由于周圍靜止流體內的壓強各處都相等,所以可以認為,整個射流區內的壓強都是一樣的;射流邊界層的內、外邊界線都是直線。
根據自由淹沒射流理論,圓形截面軸向對稱射流有以下特征:
轉折截面上射流寬度等于噴管出口直徑的3.28倍。
射流擴散角θ為270-30030'
射出能力Um=U0*0.966/(α*S/R0+0.294) α=0.07-0.08
2 自由淹沒射流理論在脈沖噴吹設計中的應用
脈沖噴吹濾袋除塵器在設計過程中,常常涉及噴管設計。噴管設計主要包括噴管形式、噴口大小、噴口高度。
噴管外表形式多種多樣,究其根本只有兩種:收縮噴管、縮放噴管。收縮噴管的流通截面是逐漸縮小的,流通截面不變的噴管本質上也屬于收縮噴管。縮放噴管的流通截面是先縮小后擴大。縮放噴管也稱拉伐爾噴管。亞音速氣流在收縮噴管內膨脹加速,不可能得到超音速流動。要得到超音速流動,必須在漸縮漸擴形的拉伐爾噴管內才能得到超音速流動。
由于當前脈沖濾袋除塵領域并未涉及超音速噴吹清灰,下面僅以收縮噴管為例進行研究。
高速壓縮空氣通過噴管對濾袋進行噴吹清灰,其速度可以達到接近臨界音速。臨界音速不是一個定值,與溫度有關。在0℃時,空氣的臨界音速為302m/s。也就是說,在普通噴管的噴口0℃時最大速度為接近302m/s。而濾袋上口凈氣流出速度一般不大于5m/s,相對于噴吹氣流可以暫時忽略。這樣,可以利用自由淹沒射流理論對噴管高度進行計算。
以φ160濾袋(籠口φ150)、噴口φ20,φ130濾袋(籠口φ120)噴口φ10為例如圖2說明:
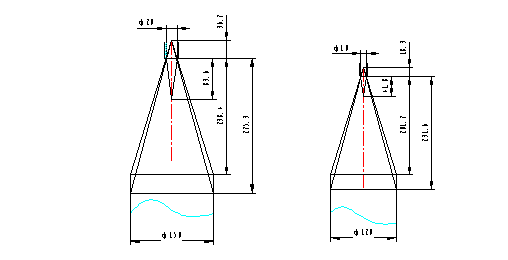
圖2 φ160和φ130濾袋噴射情況
由射流擴散角θ為270-30030',很容易計算出籠口φ150、噴口φ20時的噴吹高度在238.4-275.3之間。理論上,如果高于此高度,即有部分空氣吹到多孔板外面造成浪費。如果低于此高度,可能會造成濾袋頂部清灰不利。在實踐應用當中,因為噴管安裝偏離等其它方面原因,實際高度一般會略低于此高度。同理,可以計算出籠口φ120、噴口φ10時的噴吹高度在201.7-231.6之間。
根據公式Um=U0*0.966/(α*S/R0+0.294),可以計算袋口噴吹氣流的理論速度:
表1 袋口噴吹氣流的理論速度
|
條件:噴口速度接近302 m/s |
袋口氣流速度(m/s) |
|
籠口φ150、噴口φ20、噴吹高度230 |
約144.5 |
|
籠口φ120、噴口φ10、噴吹高度200 |
約88.5 |
因為受到袋口凈氣上升速度影響,實際速度要略小于理論計算速度。
噴吹氣體進入濾袋以后,氣體受到濾袋周壁的約束,不能繼續擴散,所以不再適用于自由淹沒射流理論進行研究。
3 自由淹沒射流理論在直通式濾袋除塵器進風口設計中的分析研究
在直通式濾袋除塵器設計時,進風口后濾袋迎風面受風速度要求嚴格,如果不能得到有效控制,很容易吹損濾袋。利用自由淹沒射流理論同樣可以分析進風口相關部位的風速結構。
以φ1000進風管道為例進行分析。如圖3,進風管道連接喇叭形進風口。
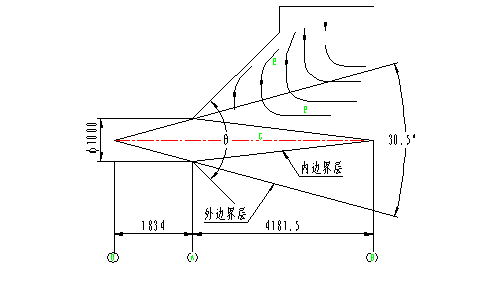
圖3 進風管喇叭形連接
氣流以管道風速U0均勻地從管口(A)流出,進入喇叭口(擴張角θ)。由于流通面積不斷擴大,在流動中周圍流體不斷摻入,射流的寬度逐漸增大,而在射流中還保持射流初速U0的區域則逐漸縮小。在離開噴管出口一定距離(4181.5)以后,保持初速U0的射流核心區就消失了。
現在討論兩種情況,喇叭口擴張角θ>30.50時(不是定值,介于27-30.50之間,為簡化分析以30.50為例,下同),如上圖所示。由于周圍流體要不斷摻入,而喇叭周壁阻擋了上下兩個方向上的氣流,所以只能由喇叭后端補充,從而在喇叭口周圍形成渦流,產生能量損失。如圖,E區為渦流區,速度為負值;F區流速介于零到管道風速之間;G區流速與管道風速相同。
由上分析可知,在喇叭口末端的流速,是不均勻的,單純用流量除以截面積所得理論平均流速并無實踐意義。要想得到均勻的流體速度,有兩個措施:一是將喇叭口做長,可以得到相對均勻設計流速。這種措施在實踐中也有應用,并非運用于直通式袋除塵器。另一種措施是加均風板,用外力減弱流體前進速度,強制補充渦流區,這種措施已經得到廣泛應用。
另一種情況是當喇叭口擴張角θ<30.50時,射流自動充滿喇叭空間,周圍靜止流體由于受到喇叭周壁的阻擋,不會有流體摻入,所以沒有渦流。這種情況不再屬于自由淹沒射流理論的研究范圍,而屬于亞音速擴壓管研究的范圍,其特征是隨著氣流的截面積增大,流速減小,壓力增大。其均風效果更有效。
所以說,在不設均風板時,喇叭口的擴張角如果高于300,是不科學的。
自由淹沒射流理論在其它地方也可以應用,譬如可以對濾袋出口的凈氣流速進行分析,分析某高度點的氣體速度,可以為凈氣室的高度設計提供理論依據。在除塵系統設計中,也有一些地方可以利用該理論進行分析研究。
選自2009全國袋式除塵技術研討會論文集 | 
